Stochastic Differential Equations

背景

在前面的笔记中，已经介绍了两种diffusion的方式

一种是以DDPM为代表的，sequentially corrupt training data with slowly increasing noise, and then learn to reverse this corruption in order to form a generative model of the data，缓慢增加噪声，然后学习扭转过程

另一种是以SMLD为代表的，Score matching with Langevin dynamics (SMLD) estimates the score (i.e., the gradient of the log probability density with respect to data) at each noise scale, and then uses Langevin dynamics to sample from a sequence of decreasing noise scales during generation，用分数匹配估计每个噪声尺度上的分数，然后用朗之万动力学从递减序列中进行采样。

而在NCSN中其实已经提到，两者之间是有联系的，损失函数本质上是一样的，论文中提到，for continuous state spaces, the DDPM training objective implicitly computes scores at each noise scale，DDPM隐式地计算每个噪声尺度的分数。

因此，宋飏博士通过随机微分方程SDE（stochastic differential equations）的视角，统一了之前的方法。

简单来说，考虑根据扩散过程随时间演变的连续分布，用不依赖于数据、没有可训练参数的SDE来将数据点扩散为随机噪声。然后训练一个网络来估计分数，最后通过近似反转SDE生成样本。

原理

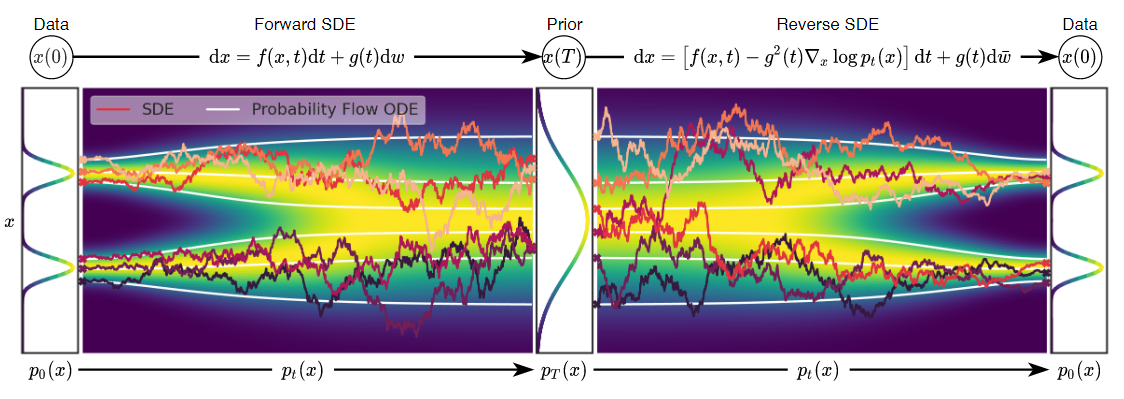
图片左侧是原数据分布，中间是噪声分布（先验），右边是生成数据的分布

先看正向SDE

$\mathsf{d}x=f(x,t)\mathsf{d}t+g(t)\mathsf{d}w$

其中，$x$ 是数据，$w$ 是标准维纳过程、布朗运动，简单来说就是个随机因子，$f(\cdot,t)$ 是一个向量函数，被称为 $x(t)$ 的漂移系数，$g(t)$ 是一个标量函数，被称为扩散系数。

与DDPM和NCSN不同的是，这里的t是一个连续变量，而非离散变量

参考【2】中的解释，SDE将原来的离散过程 $(1,2,...,T)$ 连续化成 $(0,\dfrac{1}{T},...,\dfrac{T-1}{T},1)$

由此，变换一下DDPM中的前向公式

那么，在此基础之上，反向过程的SDE可以根据下面的公式得到

$\mathsf{d}x=[f(x,t)-g(t)^2\nabla_x\log p_t(x)]\mathsf{d}t+g(t)\mathsf{d}\bar w$

DDPM对应的反向SDE就是

$\mathsf{d}x_t=-\dfrac{1}{2}\beta(t)[x_t-2\nabla_x\log q_t(x_t)]\mathsf{d}t+\sqrt{\beta(t)}\mathsf{d}\bar w_t$

这样我们就可以用一个网络来近似上面的score function了，然后根据逆向过程进行采样

而关于常微分方程ODE（ordinary differential equation），宋飏博士又在附录D中附上了每个扩散过程都有对应的确定性ODE的形式使得其边缘分布 $p_t(x)$ 与SDE一致的证明，这个ODE可以表示为

$\mathsf{d}x=[f(x,t)-\dfrac{1}{2}g(t)^2\nabla_x\log p_t(x)]\mathsf{d}t$

可以发现这个形式和SDE的形式高度相似，区别在于系数和噪音项

而两者的区别也可以通过最上面那张图展示出来，白线部分是ODE的过程，彩线部分是SDE的过程，很明显ODE的过程更稳定，而且两者最终得到的分布是一致的。

而且ODE可以用更大的步长进行求解，因此效率更高。

同时，宋飏博士还在论文中指出，我们在SDE的逆向求解过程中，借用贝叶斯定理：

后面两项都是可以估计的score function，因此我们可以通过Langevin-MCMC生成 $p(x|y)$

这样就可以根据给定条件生成指定图像了

具体训练方面，宋飏博士采用了Predictor-Corrector（PC）采样器，即反向SDE作为predictor，score-based MCMC（例如SMLD）作为corrector，两者相结合可以得到更好的表现

参考资料

[0] Score-Based Generative Modeling through Stochastic Differential Equations

[1] 扩散模型与能量模型，Score-Matching和SDE，ODE的关系 - 知乎 (zhihu.com)

[2] 一文解释 Diffusion Model (二) Score-based SDE 理论推导 - 知乎 (zhihu.com)

[3] 基于得分的随机微分方程生成建模（Score-Based Generative Modeling Through Stochastic Differential Equations） - 知乎 (zhihu.com)