Score-based Model via Langevin Dynamics

2023年05月04日 3.1k 字大概 14 分钟

Score-based Model

能量模型

根据能量模型的理论，任意一个概率分布都可以用一个更通用的形式来表示

$p_\theta(x)=\dfrac{\exp(-\mathbb{E}_\theta(x))}{Z(\theta)}$

其中，分母是归一化的配分函数

最直接的优化方法就是求MLE（Maximum Likelihood Expectation），但是由于Z的存在，无法直接优化，但是又可以利用MCMC的方法估计对数似然的梯度，得到

$\nabla_\theta\log p_\theta(x)= - \nabla_\theta\mathbb{E}_\theta(x)-\nabla_\theta\log(Z_\theta)$

第一项可以直接梯度下降，第二项可以展开得到一个无偏的单样本估计：

$\nabla_\theta\log(Z_\theta)\simeq- \nabla_\theta\mathbb{E}_\theta(\tilde x),\ \tilde x \sim p_\theta(x)$

什么是无偏估计呢？就是每个样本的概率都一样。

而这个样本是从能量模型构建的分布中采样出来的，所以只要可以从模型中采样，就可以得到这一项，因此两项都可以求。但是采样这件事本身不是很简单，宋飏博士提到了两种采样方法，Langevin MCMC和Hamiltonian Monte Carlo，都利用了对数似然对样本的梯度就是对能量函数 $\mathbb{E}$ 的负梯度这一事实，即

$\nabla_x \log p_\theta(x)= - \nabla_x \mathbb{E}_\theta(x)-\nabla_x\log(Z_\theta)=- \nabla_x \mathbb{E}_\theta(x)$

中间式中，由于第二项与x无关，所以梯度为0。

然后根据朗之万动力学采样（Langevin-MCMC）

$x^{k+1}\leftarrow x^k+\dfrac{\epsilon^2}{2}\nabla_x\log p_\theta(x^k)+\epsilon z^k, k=0,1,...,K-1$

当 $\epsilon$ 足够小且迭代步数 $K$ 足够大的情况下可以近似从 $p_\theta$ 中采样

这样我们就可以通过估计 $p_\theta$ 对输入 $x$ 的梯度（也就是所谓的score）来实现采样，从而使得MLE可求。

总结一下，我们对能量模型参数的每一次随机梯度更新，都需要使用MCMC来近似从分布里采样，来估计梯度的计算。这样做会需要大量样本，从而带来非常大的计算量。

Score Matching

用神经网络来拟合score，就是score matching，优化目标为

$D_F(p(x)\parallel p_\theta(x))=\mathbb{E}_{p}[||\nabla_x \log p(x)-s_\theta(x))||^2_2]$

Score matching 的目标就是使得真实数据分布对输入x的对数似然的梯度（score）和我们所建模的近似分布的score一致。然后，根据一阶导处处相等，且概率密度函数积分都为1，所以两个数据分布一致。

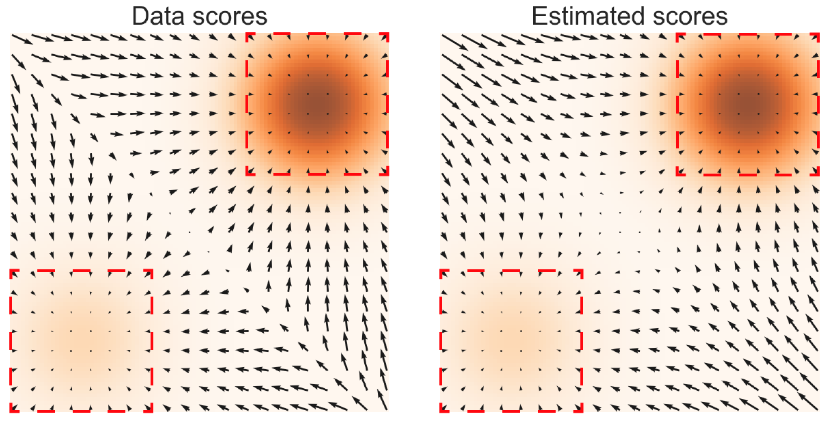
一个对score比较直观的解释就是“矢量场”，也是宋飏博士在论文中借用的可视化方式。

两个焦点意味着数据分布中心，而位于场的其余位置的数据可以通过梯度下降的方式收敛到数据分布的高概率密度区域。

但是哪怕我们直接将能量模型建模成score，然后根据训练好的能量模型的score来进行MCMC采样，也依然逃不过对分布的计算。但有大量的工作让我们可以直接计算score-matching，而不需要计算真实数据分布。同时这些方法还足够快，只涉及到一阶导数的计算。因此，效率会大大提高。

痛点

利用神经网络近似score function，然后使用朗之万动力学采样目标分布的样本，但是简单地使用上面的score matching方案会有两个问题：

大部分我们希望拟合的数据（比如图像）在高维空间里表现为低维流形。而大部分采样的点不落在低维流形上则其概率为零，对零概率的点取对数（score的定义是logP(x))无意义。
score function的优化目标是个L2范数的期望，而对于低密度的区域该期望因无法得到足够多的样本来监督训练，其准确度也不高。该问题和以上的低维流形问题一起加剧了采样结果的不理想情况。

而根据宋飏博士的论文，以上两个问题都会被往数据里添加高斯噪声所解决。

高斯噪声的定义域是整个参数空间，所以对原数据添加高斯噪声解决了低维流形的零概率问题。
添加大量的高斯噪声实质上扩展了分布里的各个众数的范围，使得数据分布里的低概率区得到了更多监督信号。

但是高斯噪声的尺度选择不是个简单的问题，加过大的噪声虽然会覆盖更多的低概率空间，但同时也会剧烈地改变原数据分布，但过小的噪声又会使得低概率空间的监督信号不足，尽管小噪声可以获得对原数据分布更好的近似。

而作者最终采用的方案是添加一系列不同尺度的噪声，并训练一个条件于噪声大小的score matching网络（noise-conditioned-score-based-model）对他们进行拟合。

原理

使用NCSN学习score function，然后使用 annealed Langevin dynamics 采样

NCSN

定义一组几格级数序列（等比数列） $\{\sigma_i\}_{i=1}^L$ ，其中 $\sigma_i>0$ 且 $\dfrac{\sigma_1}{\sigma_2}=\dfrac{\sigma_2}{\sigma_3}=\cdots=\dfrac{\sigma_{L-1}}{\sigma_{L}}>1$ ，用分布 $q_\sigma(x)=\int p(x)\mathcal{N}(x|t,\sigma^2\mathbf{I})dt$ 表示扰动噪声数据分布。

加入噪声扰动后的数据分布为 $q_\sigma(\tilde x|x)=\mathcal{N}(\tilde x|x,\sigma^2\mathbf{I})$ ，则概率密度函数为

然而 $\tilde x = x + \sigma\epsilon$ ，因此

$\nabla_{\tilde x} \log[q_\sigma(\tilde x | x)]=-\dfrac{\epsilon}{\sigma}=-\dfrac{1}{\sqrt{1-\bar\alpha_t}}\epsilon$

这其实是make sense的，因为梯度更新的方向是噪声的反方向，实质上等价于去噪的过程，所以这也是score matching和DDPM的联系，在损失函数上也是一致的。

这里引用[2]的证明：

根据Tweedie's Formula，对于一个高斯变量 $z\sim\mathcal{N}(z;\mu_z,\Sigma_z)$ ，有：

$\mu_z = z + \Sigma_z\nabla_z\log p(z)$

套用到前向过程 $x_t\sim q(x_t|x_0)=\mathcal{N}(x_t;\sqrt{\bar\alpha_t}x_0,(1-\bar\alpha_t)\mathbf{I})$ 中，得

$\sqrt{\bar\alpha_t}x_0=x_t+(1-\bar\alpha_t)\nabla_{x_t}\log p(x_t)$

做一下关于 $x_0$ 的等价变化

$x_0=\dfrac{x_t+(1-\bar\alpha_t)\nabla_{x_t}\log p(x_t)}{\sqrt{\bar\alpha_t}}=\dfrac{x_t-\sqrt{1-\bar\alpha_t}\epsilon_t}{\sqrt{\bar\alpha_t}} \rightarrow \nabla_{x_t}\log p(x_t)=-\dfrac{\epsilon_t}{\sqrt{1-\bar\alpha_t}}$

代入到DDPM中推导出来的 $\mu_q$ 中，可以得到

$\mu_q=\dfrac{1}{\sqrt{\alpha_t}}x_t+\dfrac{1-\alpha_t}{\sqrt{\alpha_t}}\nabla_{x_t}\log p(x_t)$

类似地，逆向过程可以建模为

$\mu_\theta=\dfrac{1}{\sqrt{\alpha_t}}x_t+\dfrac{1-\alpha_t}{\sqrt{\alpha_t}}s_\theta(x_t,t)$

这样DDPM中的优化目标和score matching的优化目标其实就是一致的了。

但是对于训练目标

$l(\theta,\sigma)=\mathbb{E}_{p_{\sigma}(x)}[|| \dfrac{\tilde x-x}{\sigma^2} + s_\theta(x))||^2_2]$

其关于 $\sigma$ 的量级（噪声级别）是 $\dfrac{1}{\sigma^2}$ ，受到 $\sigma$ 的大小的影响，因此如果我们对其加权，权重为 $\sigma^2$ ，那最终所有级别的噪声的损失都在同一量级，不再受大小的影响，从而保证了模型的公平性，不会过分重视或者忽视某个噪声级别所要学习的内容。因此最终的训练损失为：

$L(\theta,\{\sigma_i\}_{i=1}^L)=\dfrac{1}{L}\sum\limits_{i=1}^{L}\lambda(\sigma_i)l(\theta,\sigma_i), \ \lambda(\sigma_i)=\sigma_i^2$

在这种训练方式下，只要预先设定好 $\{\sigma_i\}_{i=1}^L$ ，然后在每次迭代时随机选取其中一个噪声级别 $\sigma_i$ ，并采样一个标准高斯噪声 $\epsilon$ ，对原始数据样本加噪： $\tilde x=x+\sigma_i\epsilon$ ，接着将加噪后的样本 $\tilde x$ 与对应的噪声级别 $\sigma_i$ 一并丢给网络得到预测的分数 $s_\theta(\tilde x,\sigma_i)$ ，然后就可以使用上述损失函数来计算损失了。

具体算法流程如下：

def anneal_dsm_score_estimation(scorenet, samples, labels, sigmas, anneal_power=2.):
    # 取出每个样本对应噪声级别下的噪声分布的标准差，即公式中的sigma_i，
    # 这里的 labels 是用于标识每个样本的噪声级别的，就是 i，实际是一种索引标识
    # (bs,)->(bs,1,1,1) 扩展至与图像一致的维度数
    used_sigmas = sigmas[labels].view(samples.shape[0], *([1] * len(samples.shape[1:])))
    # 加噪：x' = x + sigma * z (z ~ N(0,1))
    perturbed_samples = samples + torch.randn_like(samples) * used_sigmas
    
    # 目标score，本质是对数条件概率密度 log(p(x'|x)) 对噪声数据 x' 的梯度
    # 由于这里建模为高斯分布，因此可计算出结果最终如下
    target = - 1 / (used_sigmas ** 2) * (perturbed_samples - samples)
    # 模型预测的 score
    scores = scorenet(perturbed_samples, labels)
    target = target.view(target.shape[0], -1)
    scores = scores.view(scores.shape[0], -1)

    # 先计算每个样本在所有维度下分数估计的误差总和，再对所有样本求平均
    loss = 1 / 2. * ((scores - target) ** 2).sum(dim=-1) * used_sigmas.squeeze() ** anneal_power

    return loss.mean(dim=0)

Annealed Langevin Dynamics

代码如下：

def anneal_Langevin_dynamics(self, x_mod, scorenet, sigmas, n_steps_each=100, step_lr=0.00002):
    images = []

    with torch.no_grad():
        # 依次在每个噪声级别下进行朗之万动力学采样生成，噪声强度递减
        for c, sigma in tqdm.tqdm(enumerate(sigmas), total=len(sigmas), desc='annealed Langevin dynamics sampling'):
            # 噪声级别
            labels = torch.ones(x_mod.shape[0], device=x_mod.device) * c
            labels = labels.long()

            # 这个步长并非 Algorithm 1 中的 alpha，而是其中第6步的 alpha/2
            # 对应朗之万动力学采样公式(见公式(vi))的 epsilon/2
            step_size = step_lr * (sigma / sigmas[-1]) ** 2
            
            # 每个噪声级别下进行一定步数的朗之万动力学采样生成
            for s in range(n_steps_each):
                images.append(torch.clamp(x_mod, 0.0, 1.0).to('cpu'))
                # 对应朗之万公式最后一项
                noise = torch.randn_like(x_mod) * np.sqrt(step_size * 2)
                # 网络估计的分数
                grad = scorenet(x_mod, labels)
                # 朗之万动力方程
                x_mod = x_mod + step_size * grad + noise

        return images